Анализ равномерности выпадения номеров на рулетке – анализ соответствия эмпирической выборки генеральной совокупности.
Анализ отклонения фактической частоты выпадения номеров колеса рулетки по выборке от теоретической (ожидаемой) частоты 1/37 (равномерное выпадение номеров).
Цель Анализа равномерности выпадения номеров на рулетке – выявление номеров, частота выпадения которых имеет критическое отклонение, а также, подтверждение или опровержение гипотезы от том, что наблюдаемые частоты (выборка) является частью генеральной совокупности.
Анализ равномерности выпадения номеров на рулетке производится по заданной или произвольной выборке. Регистрируется частота выпадения каждого из 37-ми номеров колеса рулетки с последующим анализом равномерности выпажегия по критерию χ2.
Распределение χ2 –Chi square distribution
Распределение χ2 –Chi square distribution – является одним из наиболее широко используемых в статистике для проверки статистических гипотез. На основе распределения χ2 построен один из наиболее мощных критериев согласия – критерий χ2 Пирсона, согласно которому принимается или отклоняется Нулевая гипотеза.
Критерий согласия χ2 Пирсона
Критерий χ2 проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот.
Распределение χ2 c d.f. степенями свободы (degrees of freedom) — это распределение суммы квадратов k независимых стандартных нормальных случайных величин (d.f.=k-1).
Сумма квадратов независимых величин имеет распределение χ2 и поэтому является критерием проверки нулевой гипотезы Н0 – распределение выпадения номеров равномерно. Число степеней свободы d.f. для критерия берется на 1 меньше, чем число всего номеров на рулетке (d.f. = 37 – 1 = 36).
Частоты
Под частотой понимается количество появлений какого-либо события – количество выпадения каждого из 37 номеров на колесе Рулетки. Частота выпадений – случайная величина, распределенная по закону Бернулли.
Нулевая гипотеза
Нулевая гипотеза: отклонение фактических частот выпадения номеров на рулетке от теоретических носит случайный характер – наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, они взяты из той же генеральной совокупности), распределение выпадения номеров равномерно. Нулевая гипотеза принимается, если значение χ2 экспериментальное меньше критического значения χ2. Нулевая гипотеза Н0 принимается на уровне значимости 5% числа степеней свободы 36. Уровень значимости – задаваемый параметр.
Нулевая гипотеза – предположение, что расхождение между эмпирическими и теоретическими или ожидаемыми частотами выпадения номеров на рулетке носит случайный характер, опровергается, если χ2 выборки больше или равно χ2 критического для принятого уровня значимости 0,05 (5%) и числа степеней свободы 36.
Уровень значимости
Уровень значимости статистического χ2 теста (Significance Level) — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения по гипотезе H0), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна. В любом наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Уровень значимости – назначаемый параметр – 5% или 0,05, что означает, что с вероятностью 95% наблюдаемые частоты достоверны. Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.
Формула расчета χ2
Расчетная формула критерия χ2: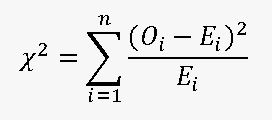
Где Oi и Ei – соответственно эмпирические и теоретические частоты.
P-value
P-value или величина, используемая при тестировании статистических гипотез. Это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-value является альтернативой классической процедуре проверки через критическое значение распределения. P-value – статистическая значимость исследуемой выборки.
P-value – Функция ХИ2.ТЕСТ возвращает вероятность того, что при условии независимости может быть получено такое значение статистики χ2, которое будет по крайней мере не меньше значения, рассчитанного по приведенной выше формуле.
Нулевая гипотеза не отклоняется, если P-value больше выбранного уровня значимости 5% (0.05), то есть частоты хорошо согласуются.
Программный модуль анализа равномерности выпадения номеров на Рулетке
Для live casino, где регистрируется 100% статистики выпадения номеров на каждой рулетке программный модуль осуществляет в автоматическом режиме обработку фактических данных статистики выпадения номеров и производит анализ выборки по критерию χ2.
Анализ производится по выборкам различной длины, в разрезе направления бросков (выборка по равнонаправленным броскам шарика (по часовой стрелке и против часовой стрелки)), в разрезе дилеров.
Модуль производит информирование в автоматическом режиме о событии риска – когда частоты выпадения номеров имеют критический, не случайный характер. Программный модуль анализа равномерности выпадения номеров на рулетке – является частью программного комплекса Risk Management для live casino.
