Выигрыш игрока после некоторой игровой серии всегда вызывает вопросы, особенно, если выигрыш значительный.
Насколько возможен такой выигрыш? Нет ли оснований для подозрения игрока в нечестной игре? Является ли выигрыш игрока случайным событием?
Есть простой математический алгоритм который позволяет ответить на все эти вопросы.
Нам необходимо рассчитать лишь два параметра: Математическое ожидание результата (Expected Value) и Стандартное отклонение (Standatd Deviation) по всей игровой сессии игрока (серии спинов) на Рулетке.
Знание двух параметров позволит нам рассчитать вероятность получить именно такой фактический результат (выигрыш игрока в абсолютном выражении) или хуже.
Для экспресс-оценки сможем рассчитать, насколько далеко лежит фактический результат игрока от математического ожидания в количестве стандартных отклонений (сигма – σ).
Итак, игрок на Рулетке играет в течение длительного времени, создавая выборку из определенного количества спинов – игровая сессия. Выборка должна быть максимально полной. Чем больше количество спинов в оцениваемой игровой сессии, тем точнее оценка результата. По итогам игровой сессии мы имеем фактический результат, который и следует оценить.
Задача: дать математическую, вероятностную оценку фактического результата игры, сделать статистический анализ результатов игры.
Решение:
- Вычислить величину Стандартного отклонения каждого спина на Рулетке.
- Вычислить величину Стандартного отклонения всей выборки – всей игровой сессии (всех спинов).
- Вычислить величину Математического Ожидания всей игровой сессии.
- Рассчитать количество в Стандартных отклонениях, на которое Фактический результат отклонился от Математического ожидания.
- Рассчитать Вероятность получить именно такой Фактический результат (проигрыш казино) или хуже.
- Провести Анализ равномерности выпадения номеров.
- Провести Анализ корреляции плотности ставок по номерам с наиболее часто выпадавшими выигрышными номерами на Рулетке.
- Сделать выводы
Математическая модель игры Рулетка обеспечивает преимущество казино 2,7% (1/37). Выигрыш казино будет стремиться к значению 2,7% от суммы всех сделанных ставок по мере увеличения количества сыгранных спинов. Такой результат достигается казино на длительной дистанции только, если:
- Выпадение любого номера на рулетке – случайное событие
- Выигрыш игрока – случайное событие.
- Каждый отдельный спин – независимое случайное событие.
Согласно Центральной Предельной Теоремы, закон распределения суммы независимых случайных величин, приближается к нормальному при достаточно большом числе слагаемых или (Теорема Ляпунова): если X1, Х2…. Xn – независимые случайные величины, имеющие одно и то же распределение с математическим ожиданием µ и дисперсией σ, то при увеличении n закон распределения суммы случайных величин неограниченно приближается к нормальному.
Таким образом, при достаточно большом количестве сыгранных на рулетке спинов, каждый из которых – независимое случайное событие, результат игры должен подчиняться Нормальному закону распределения.
Согласно Закону больших чисел, чем больше сыграно спинов, тем ближе должен быть фактический результат к математическому ожиданию.
Зная величину математического ожидания µ и дисперсию σ, мы можем рассчитать с заданной точностью доверительный интервал, в котором должен находиться фактический результат игрока с заданной точностью.
Экспресс-анализ:
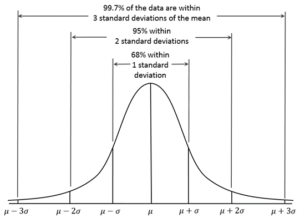
Совокупность случайных событий подчиняется Нормальному закону распределения, с которым связано правило трех сигм: 99,73% результатов случайных событий лежат в диапазоне от -3 сигма до +3 сигма от Математического ожидания, где сигма σ – величина Стандартного отклонения.
Применительно к Рулетке: μ – Математическое ожидание результата игровой сессии (серии из большого количества спинов) равно 2,7% (1/37) от суммы всех сделанных ставок во всех спинах.
Если наш фактический результат лежит выходит за рамки диапазона [μ−3σ;μ+3σ]. то вероятность такого события менее 0,27%, что должно классифицироваться, как событие риска, которое ставит под сомнение случайность результата.
Следует отметить, что условие выхода фактического результата игры за пределы диапазона [μ−3σ;μ+3σ] для регистрация события риска не является обязательным. Можно установить более чувствительные критерии (меньше чем+/-3σ) для регистрации события риска и проведения дальнейших исследований.
Остается рассчитать Стандартное отклонение игровой сессии – множества спинов на Рулетке. Как это сделать?
Два шага:
- Рассчитать Стандартное отклонение каждого отдельного спина в игровой сессии.
- Рассчитать Стандартное отклонение множества спинов (игровой сессии).
Расчет Стандартного отклонения одного спина
В каждом спине игрок делает ставки на различные позиции, ставки различной величины. В большинстве случаев “рисунок ставок” (позиции ставок, величина ставок) уникальны. Стандартное отклонение каждой отдельной ставки на рулетке: на straight up, split, street, dozens, even chances известны. Однако, когда игрок делает множество ставок на различные позиции, то эти ставки коррелированы, их нельзя рассматривать как отдельные независимые события. В этом случае множество ставок на разные позиции надо рассматривать как одну комплексную ставку, у которой есть свое математическое ожидание и стандартное отклонение (или дисперсия, которая равна квадрату Стандартного отклонения).
Для расчета величины Стандартного отклонения спина с любой конфигурацией ставок (с любым позиционным расположением) и любой величиной каждой из ставок необходимо произвести конвертацию всех ставок в номера. Преобразовать все ставки в спине в ставки в номера (straight up).
Так, ставка 200 на Split 4/7 преобразуется в две ставки в номера 4 и 7: по 100 на straight up 4 и straight up 7, а ставка на Even Chances (красное или черное) конвертируется в 18 ставок straight up в номера соответствующего цвета, в ставки величиной 1/18 ставки на шансы.
После конвертации всех ставок получим комплексную ставку игрока только на позиции straight up, в номера от 0 до 36. Вероятность выпадения каждого номера одинакова и равна 1/37. Вероятность выигрыша каждой отдельной ставки Straight up в каждом номере также равновероятна и равна 1/37. Конвертация ставок значительно упрощает расчет величины Стандартного отклонения в спине.
При выпадении номера n игрок получит выплату коэффициентом 36 к величине сделанной ставки в номере n, если ставка, сделанная в номер забирается. Это тоже самое, что игрок получит выплату с коэффициентом 35 на выигрышную ставку, которая остается у игрока, а остальные ставки проигрывают.
Результат игрока x(n) при выпадении номера n – это сумма выплаты с коэффициентом 36 к величине выигрышной ставки в номере n за вычетом суммы всех сделанных игроком ставок в спине:
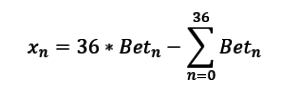
36*Bet(n) – величина выплат игроку по выигрышной ставке Bet в номере n
∑Bet(n) – общая сумма ставок игрока во всех номерах от 0 до 36 в текущем спине
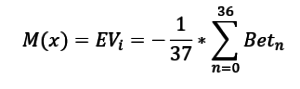
M(x)=EV(i) – Математическое ожидание результата игрока в спине i.
Формула расчета стандартного отклонения:
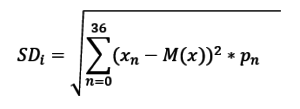
Подставим в нее значения x, M(x) и p(n):

Получим:

В итоге получаем формулу расчета Стандартного отклонения в одном спине:
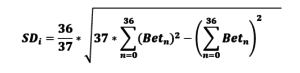
Таким образом, зная величину ставки в каждом номере от 0 до 36 (Bet(n)) и общую сумму ставок игрока в спине ∑Bet(n) на Рулетке мы можем рассчитать величину Стандартного отклонения (SD- Standard Deviation) для каждого отдельного спина i.
Если нам известно Стандартное отклонение в каждом отдельном спине, то следующий шаг – Расчет стандартного отклонения в серии спинов (полная выборка).
Расчет стандартного отклонения в серии спинов
Каждый спин – независимое случайное событие. Результат одного спина никаким образом не влияет на результат другого.
Дисперсия одного случайного события (один спин) равна квадрату Стандартного отклонения. Или Стандартное отклонение равно корню квадратному из Дисперсии:
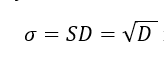
Для независимых случайных событий дисперсия нескольких независимых случайных событий равна сумме дисперсий каждого из случайных событий.
Таким образом, Стандартное отклонение результата серии из k спинов будет равно корню квадратному из суммы Дисперсий каждого спина или корню квадратному суммы квадратов Стандартных отклонений всех спинов i от 1 до k.
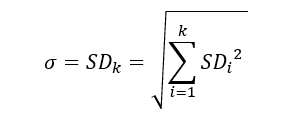
SD(i) – стандартное отклонение каждого отдельного спина i, i=1,2,3……k
SD(k) – стандартное отклонение серии из k спинов.
В Excel можно сделать таблицу, где строки – спины, а столбцы – номера рулетки от 0 до 36. Т.е. в таблицу построчно по каждому отдельному спину вносим сумму ставок в каждый номер (конвертированные в straight up ставки). По итогам каждой строки – расчет Суммы ставок в спине, Математического ожидания результата и Стандартное отклонение спина.
Получаем таблицу из k количества строк по количеству спинов в анализируемой игровой сессии. В итогах такой таблицы мы получаем Математическое ожидание результата игровой сессии и Стандартное отклонение игровой сессии – полной выборки.
Если в столбцах таблицы распределить номера в порядке, как они расположены на колесе рулетки, то итогах столбцов получаем сумму ставок в каждом номере рулетки во всех спинах. Построив гистограмму – плотность распределения ставок игрока в номера рулетки по итогам всей игры, мы увидим номера или сектора, которые наиболее плотно закрыты ставками. Гистограмма плотности распределения ставок игрока по номерам необходима для анализа корреляции ставок в номера с наиболее часто выпадавшими выигрышными номерами.
Если в итогах каждой строки по каждому спину рассчитывается Математическое ожидание и Стандартное отклонение каждого спина, то в итогах всей таблицы рассчитывается Математическое ожидание результата (1/37 от суммы всех ставок во всех спинах) и Стандартное отклонение всей игровой сессии (корень из суммы квадратов Стандартных отклонений всех отдельных спинов).
Расчет Математического Ожидания результата игровой сессии
Математическое ожидание результата игрока на Рулетке (EV или μ) по окончании определенного количества k спинов рассчитывается достаточно легко. Нужно подсчитать общую сумму ставок во всех спинах (Total Bet) и умножить на (-1/37). Т.е. при равновероятном выпадении номеров на рулетке игрок на длительной дистанции будет терять 1/37 с каждой сделанной им ставки.
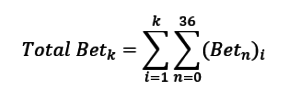
Total Bet (k) – общая сумма ставок, сделанная в k спинах
n=0,1,2…..36 – номера на рулетке от 0 до 36
i=1……k – количество спинов, сыгранных на рулетке от 1 до k
Bet (n) – величина ставки в каждом отдельном номере n
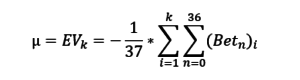
EV(k) или μ – математическое ожидание результата игрока по итогам серии из k спинов.
Анализ отклонения фактического результата от математического ожидания
Итак, по итогам игровой сессии на Рулетке состоящей из k спинов мы имеем два ключевых параметра: Математическое ожидание µ и σ Стандартное отклонение серии из k спинов.
Теперь мы можем сравнить фактический результат игровой сессии с математическим ожиданием результата и дать ему оценку.
Если фактический результат выходит за рамки диапазона [µ−3σ; µ+3σ], то фиксируем событие риска.
Рассчитаем на какое количество в Стандартных отклонениях наш фактический результат (Actual Result)отклонился от Математического ожидания. Это разница между Фактическим результатом игрока и Математическим ожиданием результата, деленная на величину Стандартного отклонения:
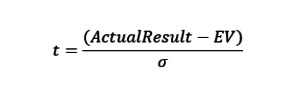
Таким образом, если -3>t>3, фактический результат выходит за рамки диапазона [µ−3σ; µ+3σ] и есть основания для дальнейшего исследования события риска.
Теперь вычислим вероятность того, что случайная величина, распределенная по нормальному закону, не превысит некоторого абсолютного значения x:
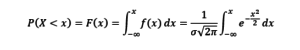
Это вероятность получить именно такой фактический результат (x – Actual Result) или хуже (вероятность попадания фактического результата в диапазон, который находится от -∞ до величины фактического результата включительно).
Если в серии спинов зафиксирован Фактический результат – Actual Result, то вероятность получить результат казино не выше, чем Actual Result (т.е. хуже) рассчитывается по формуле:
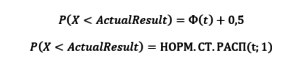
где t – величина в Стандартных отклонениях, на которую смещен Фактический результат от Математического ожидания, а
Ф(х) – функция Лапласа:
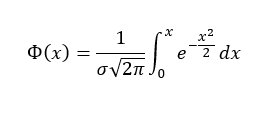
Итак, искомая вероятность:
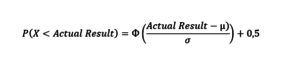
В Excel:
Ф(x)=НОРМ.РАСП(x; µ;σ;1) – 0.5
Ф(x)=НОРМ.СТ.РАСП(t;1)-0,5
Тогда
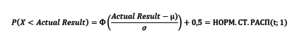
где
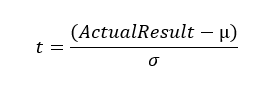
Или в Excel:

где
μ – математическое ожидание результата серии спинов
σ – стандартное отклонение серии спинов
Для общего случая: Расчет вероятности попадания фактического результата в определенный диапазон
Если Фактический результат распределен по нормальному закону:
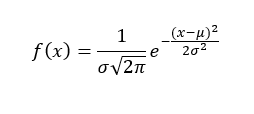
μ – математическое ожидание случайной величины x
σ – стандартное отклонение случайной величины x
То вероятность того, что Фактический результат игры на рулетке по итогам серии спинов будет отклонен от Математического ожидания на определенную абсолютную величину δ:
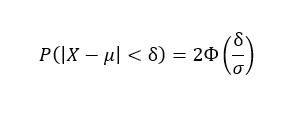
Где Ф(x) – функция Лапласа:
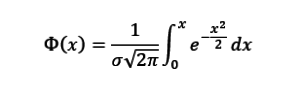
Так, вероятность того, что наш фактический результат попадет в диапазон [µ−3σ; µ+3σ]:
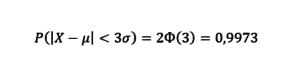
Иными словами, вероятность того, что абсолютная величина отклонения результата игры на рулетке от математического ожидания будет меньше или больше 3 стандартных отклонений очень мала и равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти.
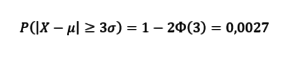
0,0027 – это вероятность выхода фактического результата из диапазона [µ−3σ; µ+3σ], т.е. выход как в плюсовую, так и в минусовую сторону. Соответственно, “односторонняя” вероятность будет в 2 раза меньше: Вероятность получить результат игры, который будет меньше Математического ожидания на -3 сигма будет 0,00135 или 0,135%.
Вероятность получить Фактический результат (Actual Result) отклонен от математического ожидания µ на t и боле стандартных отклонений рассчитывается по формуле:
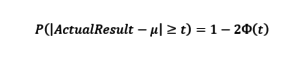
В Excel:
Ф(x)=НОРМ.РАСП(x; µ;σ;1) – 0.5
Ф(x)=НОРМ.СТ.РАСП(t;1)-0,5
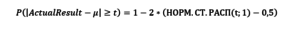
Или для общего случая, когда требуется рассчитать вероятность, того, что фактический результат попадет в абсолютных значениях в диапазон от α до β: α < X < β. Т.к. диапазон α=µ-δ β=µ+δ, где δ – абсолютная величина отклонения от математического ожидания µ.
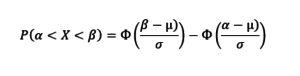
Если α=-∞, то Ф((α-µ)/σ)=Ф(-∞)=-0,5
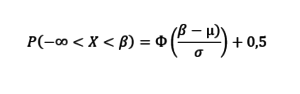
Для β= Actual Result, вероятность того что результат игры будет хуже, чем фактический Actual Result (односторонняя вероятность):

где Ф(х) – функция Лапласа.
В Excel:
Ф(x)=НОРМ.РАСП(x; µ;σ;1) – 0.5
Ф(x)=НОРМ.СТ.РАСП(t;1)-0,5
Тогда
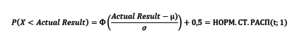
Это вероятность получить результат игры меньше значения Actual result.
Дальнейшее исследование события риска
Если по итогам игры на рулетке (серии спинов) фактический результат игры для казино отклонился на -3σ и более (-3 и более стандартных отклонения) от Математического ожидания результата μ, т.е. вероятность такого события меньше 0,135%, то есть существенные основания предположить, что результат игры не является случайным событием. Событие риска требует проведения дальнейшего анализа.
Необходимо, как минимум:
- Провести анализ равномерности выпадения номеров на Рулетке по критерию Пирсона.
Выявить наиболее часто выпадавшие номера и дать статистическую оценку частоты их выпадения. - Построить гистограмму плотности ставок по номерам рулетки. Выявить наиболее загруженные ставками номера или сектор.
Сделать анализ Корреляции между наиболее загруженными ставками номерами рулетки с наиболее часто выпадавшими выигрышными номерами.