Дисперсия – одна из основных характеристик в игре
Дисперсия случайной величины (Variance) — мера разброса значений случайной величины относительно её математического ожидания, это количественная оценка рассеивания фактических значений случайной величины относительно среднего значения.
Показатели Expected Value и House Advantage достигаются только на длительной дистанции. Фактические значения результата игры приближаются к теоретическим (расчетным) только в результате большого количества повторений случайного события. На практике, на короткой игровой дистанции, в рамках игровой сессии, фактические результаты игры ВСЕГДА отличаются от теоретических значений в той или иной мере. Дисперсия – как раз и есть мера разброса, рассеивания фактических результатов от математического ожидания. Дисперсия единичной ставки показывает в какой мере фактический результат может отклоняться от математического среднего.
Дисперсия подчеркивает вероятностный характер игры. Дисперсия – синоним азарта. Именно дисперсия позволяет игроку выигрывать в игре с отрицательным математическим ожиданием благодаря фактору волатильности и непредсказуемости каждого отдельно случайного события.
Рулетка – игра со стабильным значением House Advantage – преимущество казино неизменно по каждой ставке. На Рулетке не имеет никакого значения на какую позицию игрок делает ставку. Казино удерживает неизменную долю (процент) с каждой ставки, сделанной на Рулетке, не зависимо от позиции ставки. При этом, различные ставки на Рулетке имеют различные коэффициенты оплаты, и как следствие, имеют значительные различия по Дисперсии.
Формула расчета Дисперсии
Дисперсия случайной величины – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
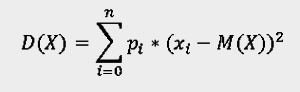
Xi — i-ое значение случайной величины, Pi— вероятность того, что случайная величина принимает значение Xi, n — количество значений случайной величины.
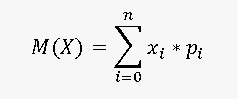
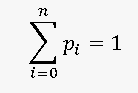
![]()
Среднеквадратичное отклонение – квадратный корень от дисперсии:
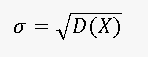
Дисперсия имеет размер квадрата случайной величины. Среднее квадратичное отклонение имеет размер случайной величины, поэтому для характеристики случайной величины часто удобнее использовать среднее квадратическое отклонение.
Зачем нам нужна Дисперсия?
Для игрока Дисперсия – это возможность выиграть! Всем игрокам известно, что в длительной игре казино всегда выигрывает, если в игре присутствует House Advantage. На короткой дистанции у игрока есть возможность выиграть, благодаря Дисперсии. Причем, чем больше Дисперсия, тем значительнее фактический результат может отличаться от теоретического среднего.
Таким образом, игрок может выбрать более дисперсионную игру, более или менее дисперсионные ставки. Дисперсия отражает степень риска, позволяет игроку выбрать игру с желаемым уровнем риска.
Игрок, имея ограниченный банк, выбирая игру и модель ведения игры (величина единичной ставки, количество hand (spin)) может с высокой вероятностью спрогнозировать диапазон, в котором будут результаты его игровой сессии.
Для казино знание Дисперсии в игре необходимо для анализа фактических результатов. Необходимо знать, в каких допустимых пределах (диапазонах) должны быть фактические результаты. Какое отклонение считается нормальным. В игре с крупными ставками, с высокой дисперсией, казино имеет риск крупного проигрыша, угрожающего платежеспособности казино. Знание Дисперсии позволяет рассчитать вероятность негативного для казино события.
Дисперсия необходима для:
- расчета кассовых резервов
- управления лимитами ставок
- разработки маркетинговых акций
- для расчета dicount с проигрыша