Баккара – игра со стабильным математическим ожиданием (Expected Value) каждой из ставок, игра с одним из самых низких показателей House Advantage и наименьшей дисперсией из всех основных игр казино.
Расчет математического ожидания, дисперсии и среднеквадратичного отклонения ставок на Баккаре
На Баккаре три основные ставки: PLAYER, BANKER, TIE 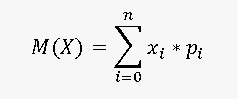
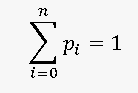
![]()
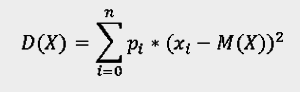
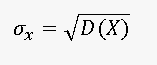
| Bet | M(X) | D(X) | SD(X) |
| BANKER | 0,0105791 | 0,86002 | 0,9273720 |
| PLAYER | 0,0123508 | 0,90469 | 0,9511527 |
| TIE | 0,143596 | 6,97421 | 2,6408726 |
| BANKER | ||||
| Bet | x | p | xp | x²P |
| Banker | 0,95 | 0,4585974 | 0,4356675 | 0,41388415 |
| Player | -1 | 0,4462466 | -0,4462466 | 0,4462466 |
| Tie | 0 | 0,095156 | 0 | 0 |
| ∑ | 1 | -0,0105791 | 0,86013075 | |
| EV= | 0,0105791 | D= | 0,86002 | |
| SD= | 0,92737 | |||
| PLAYER | ||||
| Bet | x | p | xp | x²P |
| Banker | -1 | 0,4585974 | -0,4585974 | 0,4585974 |
| Player | 1 | 0,4462466 | 0,4462466 | 0,4462466 |
| Tie | 0 | 0,095156 | 0 | 0 |
| ∑ | 1 | -0,0123508 | 0,904844 | |
| EV= | 0,0123508 | D= | 0,9046915 | |
| SD= | 0,9511527 | |||
| TIE | ||||
| Bet | x | p | xp | x²P |
| Banker | -1 | 0,4585974 | -0,4585974 | 0,4585974 |
| Player | -1 | 0,4462466 | -0,4462466 | 0,4462466 |
| Tie | 8 | 0,095156 | 0,761248 | 6,089984 |
| ∑ | 1 | -0,143596 | 6,994828 | |
| EV= | 0,143596 | D= | 6,97421 | |
| SD= | 2,64087 | |||
Графики среднеквадратичного отклонения ставки Banker
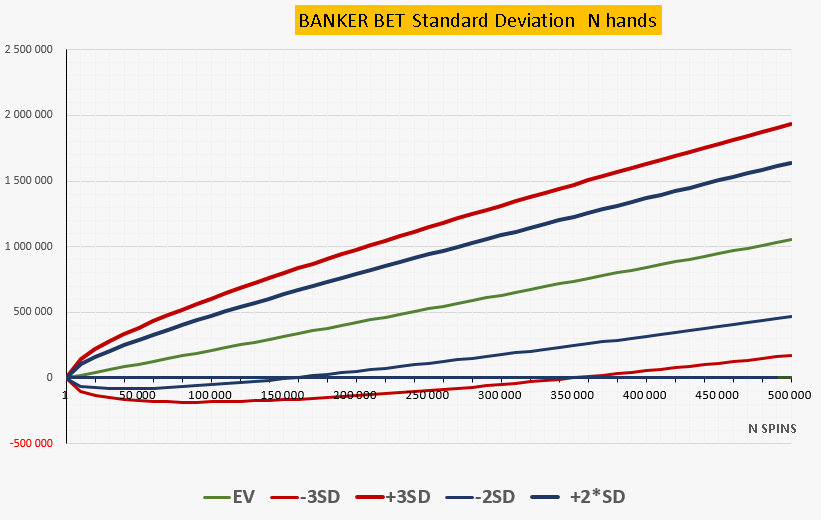
| Standard Deviation of N hands | ||||||
| BANKER BET | ||||||
| Confidence Limits | +/-3σ | 99,73% | ||||
| +/-2σ | 95,45% | |||||
| N | SD | EV-3σ | EV-2σ | EV | EV+2σ | EV-3σ |
| 1 | 0,9273 | -2,77 | -1,84 | 0,01053 | 1,87 | 2,79 |
| 100 | 9 | -26,77 | -17,49 | 1,053 | 20 | 29 |
| 1000 | 29 | -77,4 | -48,1 | 11 | 69 | 99 |
| 10 000 | 93 | -173 | -80 | 105 | 291 | 384 |
| 32 000 | 166 | -161 | 5 | 337 | 669 | 835 |
| 70 000 | 245 | 1 | 246 | 737 | 1 228 | 1 473 |
| 100 000 | 293 | 173 | 466 | 1053 | 1 640 | 1 933 |
При увеличении числа спинов EV растет прямо пропорционально количеству хэндов (раздач) EV=Wager*N*(0.01053) – на графике: зеленая прямая. Стандартное отклонение также растет при увеличении количества хэндов пропорционально квадратному корню из количества хэндов: SD=SD1*√N, где SD1-СКО единичной ставки в одном хэнде. На графике +/-3SD представлено рассеивание результата игры от среднего значения (EV) в диапазоне +/-3σ, в который попадают 99,73% всех фактических результатов. График +/2SD – область рассеивания +/-2σ -аккумулирует 95,45% фактических результатов.
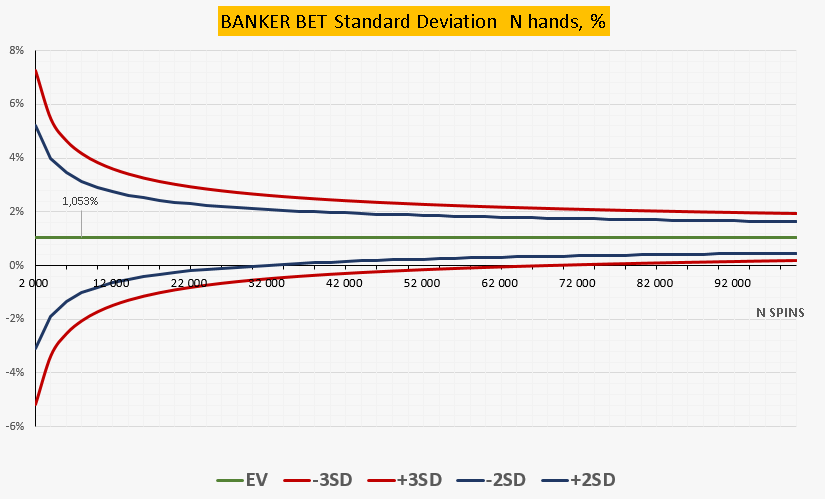
| Standard Deviation of N hands, % | ||||||
| BANKER BET | ||||||
| Confidence Limits | +/-3σ | 99,73% | ||||
| +/-2σ | 95,45% | |||||
| N | SD | EV-3σ | EV-2σ | EV | EV+2σ | EV-3σ |
| 1 | 92,735% | -277% | -184% | 1,053% | 187% | 279% |
| 100 | 9,273% | -26,8% | -17,5% | 1,053% | 19,6% | 28,9% |
| 1 000 | 2,933% | -7,745% | -4,81% | 1,053% | 6,92% | 9,85% |
| 10 000 | 0,927% | -1,729% | -0,80% | 1,053% | 2,91% | 3,84% |
| 32 000 | 0,518% | -0,502% | 0,016% | 1,053% | 2,09% | 2,61% |
| 70 000 | 0,351% | 0,001% | 0,352% | 1,053% | 1,75% | 2,11% |
| 100 000 | 0,293% | 0,173% | 0,466% | 1,053% | 1,64% | 1,93% |
В абсолютном значении EV растет быстрее, чем SD. В относительном измерении (%) EV(%)=1.053%-const. Процент удержания со ставки в отдельном хэнде (раздаче) равен 1,053% остается постоянным в каждом из N спинов, независимо от величины ставки. СКО (σ)– SD(%) в относительном измерении при увеличении количества хэндов N снижается и приближается к EV(%)=1,053%. Таким образом, график демонстрирует, что на длительной дистанции, при увеличении количества сыгранных раздач на одну и ту же позицию, N рассеивание σ% фактических результатов снижается, приближаясь к математически среднему значению EV%.
Графики поведения EV и SD ставки Banker показывают, что на короткой дистанции при всегда стабильно положительном среднем ожидаемом результате EV, фактические результаты казино могут быть отрицательными – казино может проиграть на короткой дистанции – область ниже нуля. Ставка Tie является более дисперисонной, чем Player и Banker. Ставки Player и Banker примерно равны как по величине математического ожидания, так и по среднеквадратичному отклонению. При длительной игре ставками на Banker фактические результаты казино лежат в положительной области, начиная с 32000 хэнда (hand), с вероятностью 95.45% (+/-2σ) и с вероятностью 99,73% (+/-3σ), начиная с 70000 хэнда (hand). Величина СКО (Standard Deviation, σ) – отражает уровень риска ставки, позволяет вычислить диапазон разброса фактических результатов от среднего математически ожидаемого значения на любой дистанции (любое N хэндов) с заданной вероятностью. В абсолютных цифрах: игра ставкой 1000$ на позицию Banker в течение 1000 спинов позволяет казино с вероятностью 99,73% ожидать результат в диапазоне от-77446$ до +98506$ и с вероятностью 95,45% ожидать результат в диапазоне: -48121$ до +69181$ Игра такой же ставкой 1000$, на той же позиции, но в течение 100000 спинов позволяет казино с вероятностью 99,73% ожидать результат в положительном диапазоне от+173240$ до +1932760$.
СКО на Баккаре и Рулетке
Важно отметить, что ставки Player/Banker весьма схожие со ставками Red/Black на рулетке имеют значительные различия по поведению области рассеивания. Ставка Player и любая из ставок Even Chances имеют одинаковый коэффициент оплаты 1:1 и почти идентичное по значению СКО (SDplayer=0.95113 ≈ SDred=0999635). Равенство СКО – означает идентичные по площади области рассеивания. Однако поведение областей рассеивания данных ставок существенно отличаются на Баккаре и Рулетке.
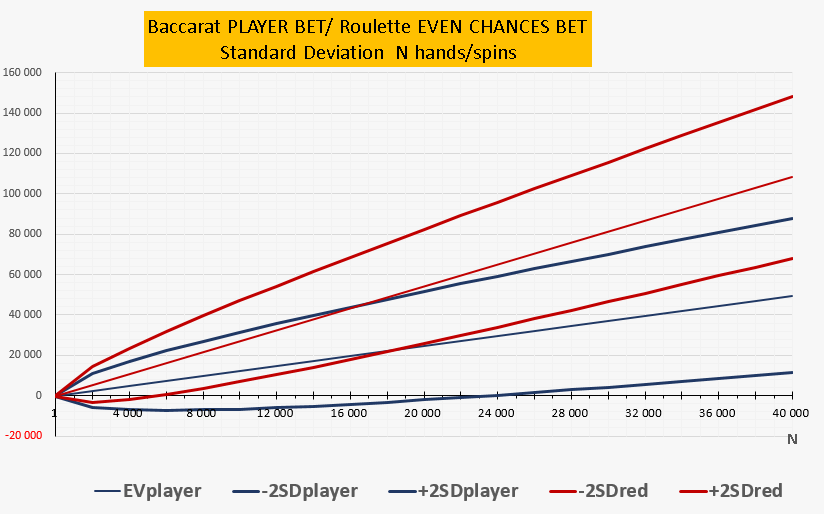
На рулетке диапазон рассеивания фактических результатов по ставкам на равные шансы (even chances) выходит в положительную область намного раньше (c 5472 спина), чем ставка Player (после 23535 хэндов!). Причина – существенное различие в величине Expected Value, которое на рулетке составляет стабильные 2,7% против 1,25% на Баккаре (ставка Player) – на графике красная прямая (Рулетка и синяя прямая (Баккара). В относительном измерении к единичной ставке или в процентах значение EV определяет на графике угол наклона прямой EV и всей зоны рассеивания SD. Зона рассеивания на Баккаре имеет угол наклона меньше, чем на Рулетке, именно по этому фактические результаты казино на Баккаре выходят в положительную область значительно позже.
Знание дисперсии и СКО имеет ключевое значение в расчетах Discount с проигрыша, Rebate on actual loss, Junket программ, а также для определения лимитов ставок для VIP игры, расчета кассовых резервов казино, оценки рисков.
Баккара, как игра с низким показателем преимущества казино (House Advantage) и низкой дисперсией, наиболее часто используется игроками для отыгрыша Wager по Бонусам в онлайн казино.
